任意の分布に関して乱数を作りたかったのでメモ。
どんな(一価の)関数にも適用出来る
アルゴリズムが作りやすい
といった理由でここでは棄却法を使います。
以下のページを参考にしています。数値計算法 2011/6/29 (pdf) 15 乱数とモンテカルロ法 (pdf)
von Neumannの棄却法
考え方はとてもシンプルで、
分布関数を含む範囲内で一様乱数のペア (
具体的には分布関数の範囲を
を作る。
生成した乱数ペア(
アルゴリズム的にはこんな感じ?(コード中にあるテストファイルはこちらから→”random_dist.txt “)#!/opt/local/bin/python
import numpy as np
from scipy.interpolate import interp1d
def randomgen(func,func_range,func_max):
while(1):
x_rand, y_rand = np.random.random(2)
x = func_range[0] + (func_range[1]-func_range[0]) * x_rand
if ( func_max * y_rand <= func(x) ):
return x
random_dist = np.loadtxt('random_dist.txt') # load function
func = interp1d(random_dist[:,0],random_dist[:,1],kind='linear') # interpolate
func_range = [min(random_dist[:,0]),max(random_dist[:,0])] # holizontal range [x_min, x_max]
func_max = max(random_dist[:,1]) # vertical range
# generate random number list
xlist = []
for i in range(1000):
xlist.append(randomgen(func,func_range,func_max))
# plot result
histresult = hist(xlist, range=[func_range[0],func_range[1]], bins=30, color='red', alpha=0.5)
plot(random_dist[:,0],random_dist[:,1]*max(histresult[0])/max(random_dist[:,1])),color='blue',linewidth=2.0)
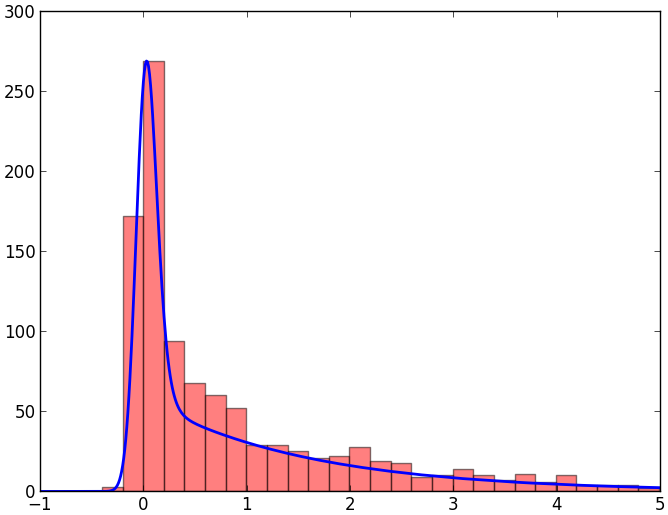
結果のヒストグラム:
)を生成
) が分布関数内に入っていれば、
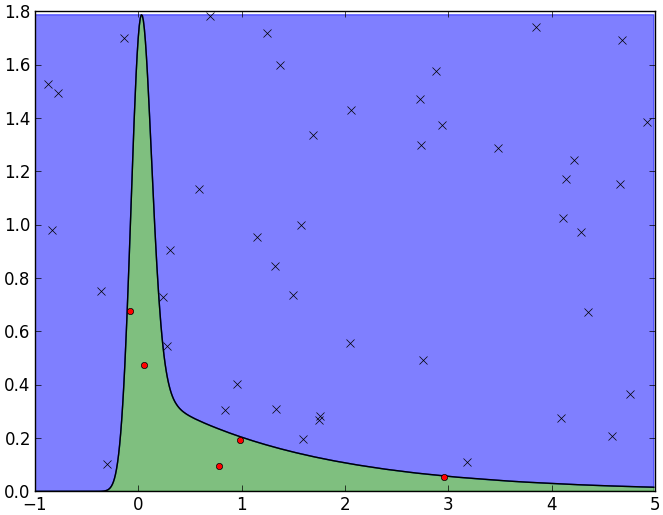
を分布に従う乱数として採用(下図でいうと赤点が採用、×が不採用)
、
を
に従う一様分布と仮定した時に、