月別アーカイブ: 2012年11月

超新星のSEDから光度曲線を計算（Example編）

投稿日時: 投稿者:
返信

 

「超新星のSEDから光度曲線を計算」でNugent templateを使って計算した光度曲先例。
Bバンド最大光度は、以下を参考。
A Comparative Study of the Absolute Magnitude Distributions of Supernovae
Richardson et al. 2002（ADS）
# Habble定数がH_0=60[{\rm km }{\rm s}^{-1} {\rm Mpc}^{-1}] になってるので注意。例えばH_0=70に変換する時は、
\displaystyle 5\log_{10}(\frac{70}{60})を加えること。

 

Ia型超新星（z=0.0, 0.5, 1.0）


 

Ibc型超新星（z=0.0）


 

IIL型超新星（z=0.0）


 

IIP型超新星（z=0.0）


 

IIn型超新星（z=0.0）


 

color evolution

超新星のSEDから光度曲線を計算

投稿日時: 投稿者:
返信

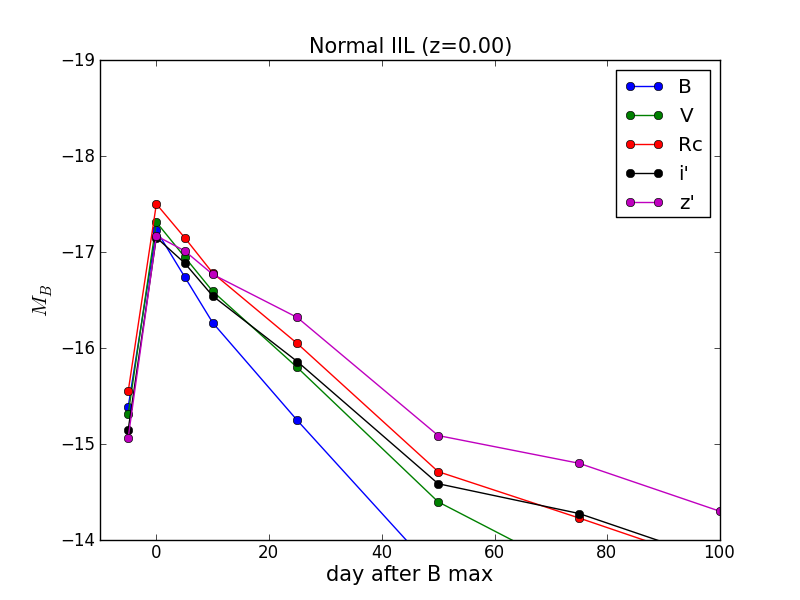
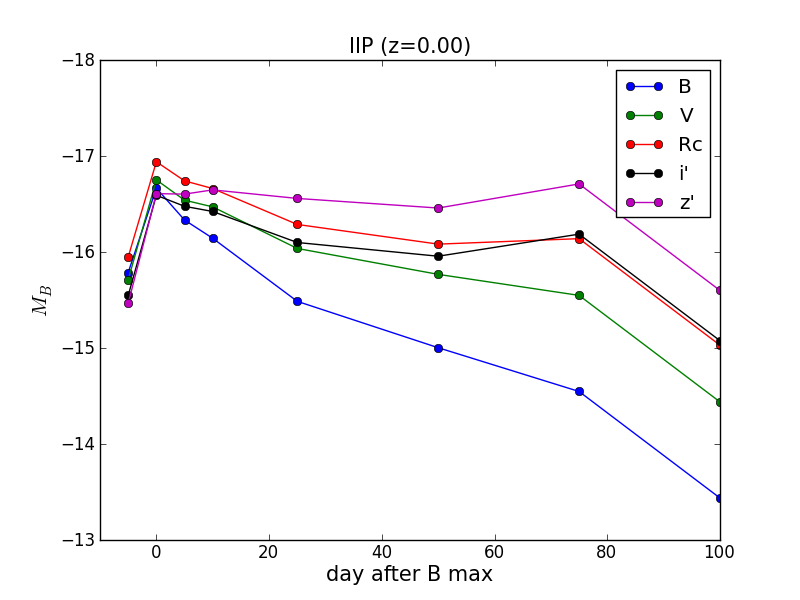
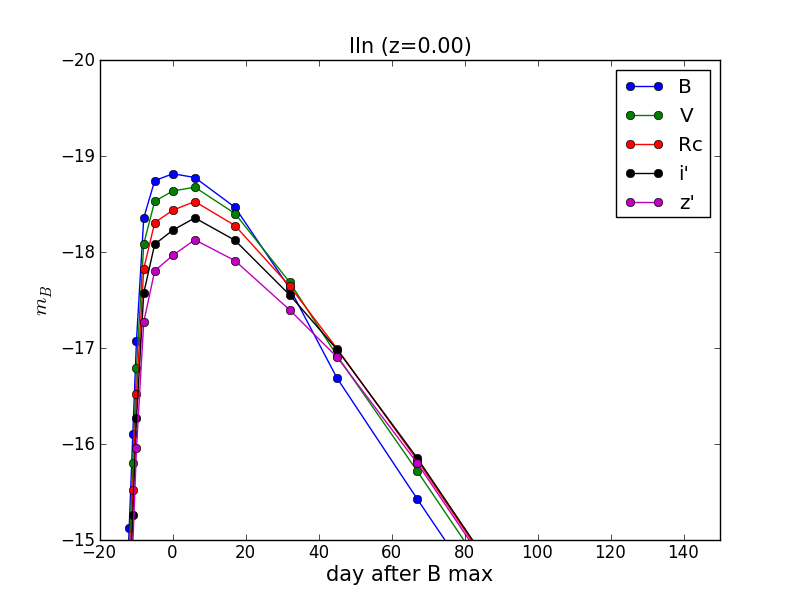
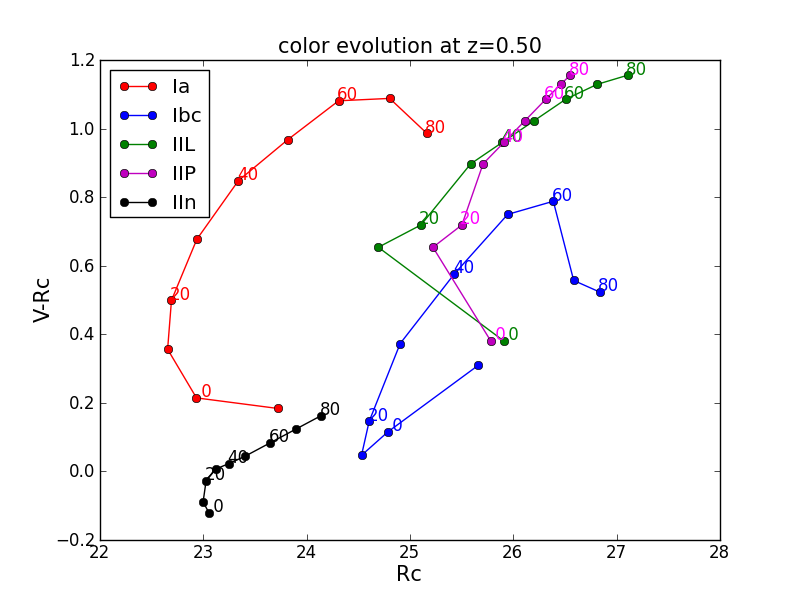
計算式については「天体のfluxからBroad-band magnitudeを計算」を参照。
 

超新星のtemplate SED

Ia型はEric HsiaoのHPからダウンロード可能。
Peter NugentのHPからも、Type Ia 1991T-like, Type Ia 1991bg-like, Type Ib/c, Type Ib/c high-velocity, Type IIP, Type IIL, Type IInなどの各種templateが手に入る。
 

Filter Response

ここでは、Suprime-Cam Filtersをここからダウンロードして使っています。
# 使っているレスポンスは「フィルター + CCD + 主鏡反射率 + 主焦点補正光学系 + 大気透過率(secz=1.2) 」のもの。
 

計算手順

以下、HsiaoのType Ia template（snflux_1a.dat）をもとに光度曲線を計算する。

  1. まずHsiaoのtemplateでは-20日から85日までのSEDが一つのファイルにまとまっているので、あらかじめspectrum_m20d.dat, spectrum_m19d.dat,…, spectrum_m01d.dat, spectrum_p00d.dat, spectrum_p01d.dat,…, spectrum_p85d.datのように各日毎にファイルを分離しておく。
  2. 後はABMAGの計算式、
    \displaystyle {\rm ABMAG}(R)=-2.5\log_{10}\frac{\int f_{\nu}\frac{R}{\nu}d\nu}{\int \frac{R}{\nu}d\nu}-48.6
    に従って計算するだけ。ただし、z>0の計算をする場合はスペクトルと時間が波長方向に(1+z)倍に伸びるので注意すること。

その他詳しい計算などは
K‐Corrections and Extinction Corrections for Type Ia Supernovae
Nugent et al. 2002 (ADS)
を参照。
 

コード例

distance modulusの計算にはPythonの宇宙論パッケージCosmoloPyを使用。
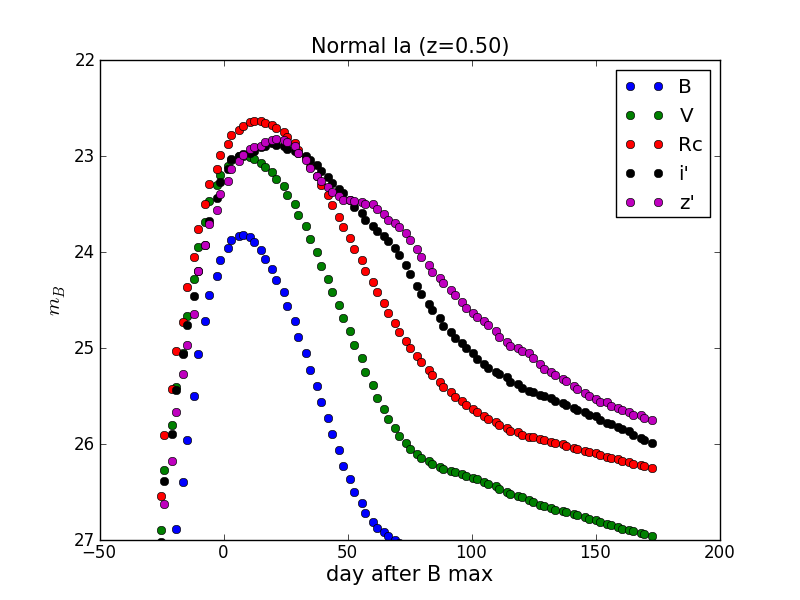
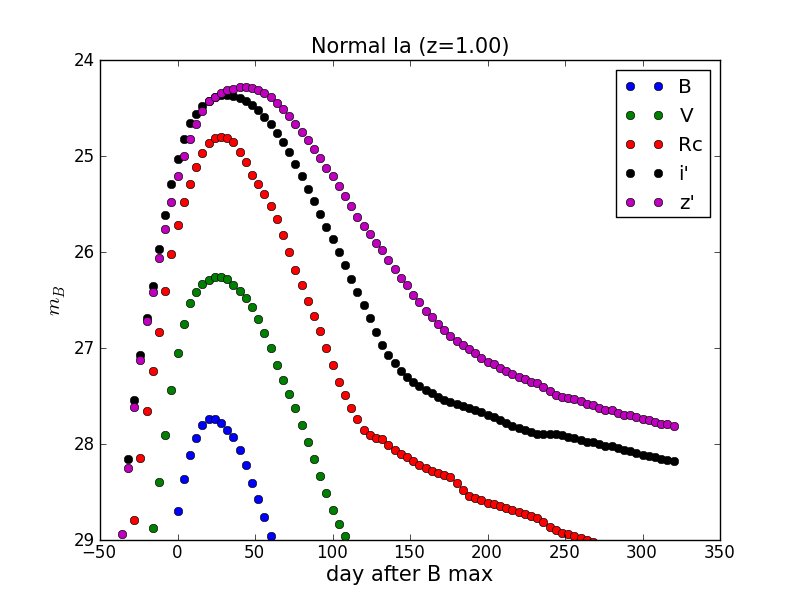
ここではVバンド絶対等級で-19.2のIa型超新星がSubaru/SCのB-,V-,Rc-,i’-,z’-bandでどのように観測されるかを計算している。

import numpy as np
import scipy.interpolate
import cosmolopy.distance as cosmocd

# convert wavelength to frequency
def convert_nu(filter):
    filter_lam=filter[:,0]*1.0e-8 # [cm]
    filter_nu=np.array([0.0] * len(filter_lam))
    for i in range(len(filter_lam)):
        filter_nu[i]=c/filter_lam[len(filter_lam)-1-i] # [Hz]
    return filter_nu*1.0e-15

# convert f_lambda to f_nu
def convert_fnu(filter):
    filter_lam=filter[:,0]*1.0e-8 # [cm]
    filter_responce=np.array([0.0] * len(filter_lam))
    for i in range(len(filter_lam)):
        filter_responce[i]=filter[len(filter_lam)-1-i,1]
    return filter_responce

# calculate ABmag
def abmagnitude(model_nu15,model_fnu,filter_nu15,filter_responce,z):
    flux=scipy.interpolate.interp1d(model_nu15,model_fnu,kind="linear")
    numerator=0.0
    denominator=0.0
    for i in range(len(filter_nu15)-1):
        for j in range(len(model_fnu)):
            if (filter_nu15[i]*(1.+z) = model_nu15[j-1]):
                dnu=(filter_nu15[i+1]-filter_nu15[i])
                numerator+=flux(filter_nu15[i]*(1.+z))*(1.+z)*filter_responce[i]/filter_nu15[i]*dnu
                denominator+=filter_responce[i]/filter_nu15[i]*dnu
    mag=-2.5*np.log10(numerator/denominator)-48.6
    return mag

# cosmological parameters
cosmo = {'omega_M_0':0.3, 'omega_lambda_0':0.7, 'omega_k_0':0.0, 'h':0.70}
# speed of light [cm s-1]
c = 2.989e10
# absolute V-band magnitude
MaV=-19.2

# load filter information
Bfilter=np.loadtxt('B-bandレスポンスファイル')
Vfilter=np.loadtxt('V-bandレスポンスファイル')
Rfilter=np.loadtxt('R-bandレスポンスファイル')
ifilter=np.loadtxt('i-bandレスポンスファイル')
zfilter=np.loadtxt('z-bandレスポンスファイル')

# define responce (as a function of nu)
Bfilter_nu15=convert_nu(Bfilter) # [E-15 Hz]
Bfilter_responce=convert_fnu(Bfilter)
Vfilter_nu15=convert_nu(Vfilter) # [E-15 Hz]
Vfilter_responce=convert_fnu(Vfilter)
Rfilter_nu15=convert_nu(Rfilter) # [E-15 Hz]
Rfilter_responce=convert_fnu(Rfilter)
ifilter_nu15=convert_nu(ifilter) # [E-15 Hz]
ifilter_responce=convert_fnu(ifilter)
zfilter_nu15=convert_nu(zfilter) # [E-15 Hz]
zfilter_responce=convert_fnu(zfilter)

# calculate AB magnitude from z=0 to z=1.2 in dz=0.05 interval
for z in np.arange(0.0,1.21,0.05):
    fout=open('z%03d' % (z*100.0),'w')
    if z>0:
        comoving_distance=cosmocd.comoving_distance(z, **cosmo) # comoving distance [Mpc]
        distance_modulus=5.*np.log10(comoving_distance)+5.*np.log10(1.+z)+25.
    else:
        comoving_distance=0.0
        distance_modulus=0.0
    # epoch loop
    for epoch in np.arange(-20,86,1):
        if epoch < 0:
            specdata='spectrum_m%02d.dat' % -epoch
        else:
            specdata='spectrum_p%02d.dat' % epoch
        model_lam=np.loadtxt(specdata)[:,0]*1.0e-8 # [cm]
        model_flam=np.loadtxt(specdata)[:,1]
        NBIN=len(model_lam)
        model_fnu= np.array([0.0] * NBIN)
        model_nu= np.array([0.0] * NBIN)
        for i in range(NBIN):
            model_fnu[i]=model_lam[NBIN-1-i]*model_lam[NBIN-1-i]*(model_flam[NBIN-1-i]*1.0e8)/c
            model_nu[i]=c/model_lam[NBIN-1-i]
        model_nu15=model_nu*1.0e-15
        # integration
        Bmag=abmagnitude(model_nu15,model_fnu,Bfilter_nu15,Bfilter_responce,z)+MaV+distance_modulus
        Vmag=abmagnitude(model_nu15,model_fnu,Vfilter_nu15,Vfilter_responce,z)+MaV+distance_modulus
        Rmag=abmagnitude(model_nu15,model_fnu,Rfilter_nu15,Rfilter_responce,z)+MaV+distance_modulus
        imag=abmagnitude(model_nu15,model_fnu,ifilter_nu15,ifilter_responce,z)+MaV+distance_modulus
        zmag=abmagnitude(model_nu15,model_fnu,zfilter_nu15,zfilter_responce,z)+MaV+distance_modulus
        print '%4.3f %5.1f %6.3f %6.3f %6.3f %6.3f %6.3f' % (z,epoch*(1.+z),Bmag,Vmag,Rmag,imag,zmag)

天体のfluxからBroad-band magnitudeを計算

投稿日時: 投稿者:
返信

 

一度ちゃんとまとめておきたかったのでメモ。内容はLBLのNaoさんが院生時代に使っていたものを参考にしています。

まず、等級は天体のflux f_{\lambda}, reference spectrum f_{\lambda}^{*}, fileter response R(\lambda), reference magnitude m_R^{*}を用いて以下のように定義できる。

\displaystyle m_R=-2.5\log_{10}\frac{\int \lambda f_{\lambda}R(\lambda)d\lambda}{\int \lambda f_{\lambda}^{*}R(\lambda)d\lambda}+m_{R}^{*}

Vega Mag, ST Mag, AB Magのうち、Vega MagはreferenceにVega fluxを使ったもの、ST MagとAB Magはreferenceとして一定のf_{\lambda}, f_{\nu}を使ったものと定義されている。詳しくは以下。

VEGAmag : Magnitude system where Vega has magnitude 0 at all wavelengths by definition. The vega magnitude of a star with flux F is -2.5 log10 (F/F_vega) where F_vega is the current flux spectrum of Vega from the CALSPEC archive.
STmag and ABmag: Both systems define the absolute physical flux density for a point source. The conversion is chosen so that the magnitude at V corresponds roughly to that in the Johnson system. In the STmag system, the flux density is expressed per unit wavelength, while in the ABmag system, the flux density is expressed per unit frequency.
Hubble Space Telescope ACS Flux Calibration and Zeropointsから引用。

 
 

f_{\lambda} based magnitude: ST Mag (Koorneef et al. 1986)

ST Magはf_{\lambda}^{*}=3.63078 \times 10^{-9} [{\rm erg } {\rm cm }^{-2} s^{-1} {\rm \AA}^{-1}]で固定したもの。

このfluxでSTMAGが0になるようにするには、

\displaystyle m_R^{*}=-2.5\log_{10}(f_{\lambda}^{*})=-21.10

であればいいので、STMagは以下のように計算出来る。

\displaystyle {\rm STMAG}(R)=-2.5\log_{10}\frac{\int \lambda f_{\lambda}Rd\lambda}{\int \lambda Rd\lambda}-21.10
 
 

f_{\nu} based magnitude: AB Mag (Oke 1964)

AB Magはf_{\nu}^{*}=3.63078 \times 10^{-20} [{\rm erg } {\rm cm }^{-2} s^{-1} {\rm Hz}^{-1}]で固定したもの。

一番最初の定義式に戻って\lambdaから\nuを以下のように変数変換する。

\displaystyle \lambda=\frac{c}{\nu} \displaystyle f_{\lambda}=f_{\nu}\frac{d\nu}{d\lambda}=f_{\nu}\frac{c}{\lambda^2}

ABMAGが0になるようにするには、

\displaystyle m_R^{*}=-2.5\log_{10}(f_{\nu}^{*})=-48.6

であればいいので、結局ABMAGは以下のように計算出来る。

\displaystyle {\rm ABMAG}(R)=-2.5\log_{10}\frac{\int f_{\nu}\frac{R}{\nu}d\nu}{\int \frac{R}{\nu}d\nu}-48.6
 

また、ABMAG⇄STMAGのconversionは（上記の変数変換を使って）計算すると以下のようになる。

\displaystyle {\rm ABMAG}(R)-{\rm STMAG}(R)=-2.5\log_{10}\frac{\int \lambda Rd\lambda}{\int \frac{R}{\lambda}d\lambda}+18.69

 
これによって、ABMAGを\lambdaで表すことも可能。

\displaystyle {\rm ABMAG}(R)={\rm STMAG}(R)-2.5\log_{10}\frac{\int \lambda Rd\lambda}{\int \frac{R}{\lambda}d\lambda}+18.69\\ =-2.5\log_{10}\frac{\int \lambda f_{\lambda}Rd\lambda}{\int \lambda Rd\lambda}-21.10-2.5\log_{10}\frac{\int \lambda Rd\lambda}{\int \frac{R}{\lambda}d\lambda}+18.69\\ =-2.5\log_{10}\frac{\int \lambda f_{\lambda}Rd\lambda}{\int \frac{R}{\lambda}d\lambda}-2.408
 
 

Vega magnitude

最初の定義によりVega magnitudeは、

\displaystyle {\rm Vega Mag}=-2.5\log_{10}\frac{\int \lambda f_{\lambda}Rd\lambda}{\int \lambda f_{\lambda}^{Vega}Rd\lambda}+0.0

なので、

\displaystyle {\rm ABMAG}-{\rm Vega Mag}=-2.5\log_{10}\frac{\int \lambda f_{\lambda}^{Vega}Rd\lambda}{\int \frac{R}{\lambda}d\lambda}-2.408

従って、

\displaystyle {\rm ABMAG}(R)={\rm Vega Mag}-2.5\log_{10}\frac{\int \lambda f_{\lambda}^{Vega}Rd\lambda}{\int \frac{R}{\lambda}d\lambda}-2.408

wordpressにWP Latex、SyntaxHighlighter Evolvedを導入

投稿日時: 投稿者:
返信

研究メモに使えそうなのでLatexプラグイン「WP Latex」と「SyntaxHighlighter Evolved」を入れてみた。

WP Latex

使い方は[ latex ]と[ /latex ]でくくった部分にtexコマンドを打ち込むだけ。以下のオプションが利用可能。

オプション 説明 例
color 色の変更 color=”000000″
background 背景色の変更
size サイズの変更（可能なサイズは-4から4まで）0がnormal size（12pt） size=”4″

例えば

[ latex size="4" ]\displaystyle \int ^{\infty}_{-\infty} e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}[ /latex ]

と入力すれば以下のように表示される（入力の際[]内のスペースは無視）。
\displaystyle \int ^{\infty}_{-\infty} e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}

その他詳しい説明はWP LaTeX FAQ参照。

SyntaxHighlighter Evolved

コードも貼りたいのでSyntaxHighlighter Evolvedもインストール。使い方は同様に[ python ][ /python ]などでソースコードを囲むだけ。

from itertools import count
from math import sqrt

def prime_gen():
    primes = []
    for n in count(2):
        if all(n%p for p in primes if p <= sqrt(n)):
            primes.append(n)
            yield n

g = prime_gen()
for i in xrange(1000):
    print g.next()

References:
ソースコードをキレイに表示するWordPressプラグイン「SyntaxHighlighter Evolved」
Clojure prime numbers lazy sequence