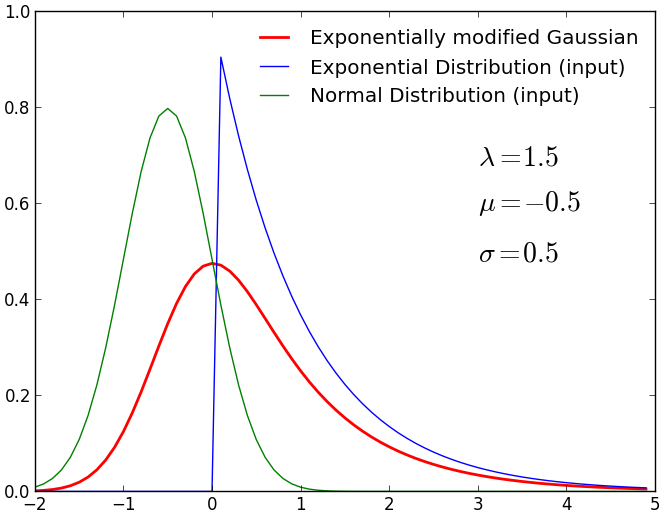
任意の分布に関して乱数を作りたかったのでメモ。
分布の逆関数を容易に求められる場合は、逆関数法を使ってしまうのが簡単なのだけど、
- どんな(一価の)関数にも適用出来る
- アルゴリズムが作りやすい
といった理由でここでは棄却法を使います。
以下のページを参考にしています。
数値計算法 2011/6/29 (pdf)
15 乱数とモンテカルロ法 (pdf)
von Neumannの棄却法
考え方はとてもシンプルで、
- 分布関数を含む範囲内で一様乱数のペア (
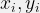 )を生成
)を生成
具体的には分布関数の範囲を![[x_{min}, x_{max}], [0, y_{max}] [x_{min}, x_{max}], [0, y_{max}]](http://s0.wp.com/latex.php?latex=%5Bx_%7Bmin%7D%2C+x_%7Bmax%7D%5D%2C+%5B0%2C+y_%7Bmax%7D%5D&bg=f1f1f1&fg=000000&s=1) 、
、
確率変数  を
を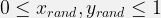 に従う一様分布と仮定した時に、
に従う一様分布と仮定した時に、
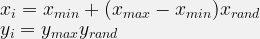
を作る。
- 生成した乱数ペア(
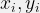 ) が分布関数内に入っていれば、
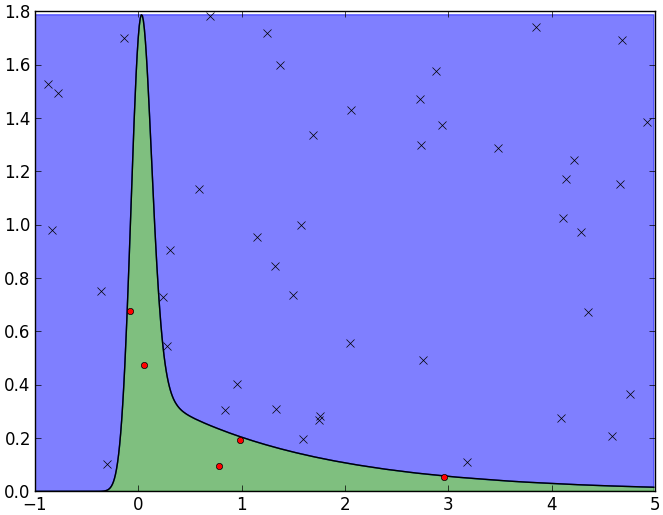
) が分布関数内に入っていれば、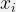 を分布に従う乱数として採用(下図でいうと赤点が採用、×が不採用)
を分布に従う乱数として採用(下図でいうと赤点が採用、×が不採用)
アルゴリズム的にはこんな感じ?(コード中にあるテストファイルはこちらから→”random_dist.txt“)
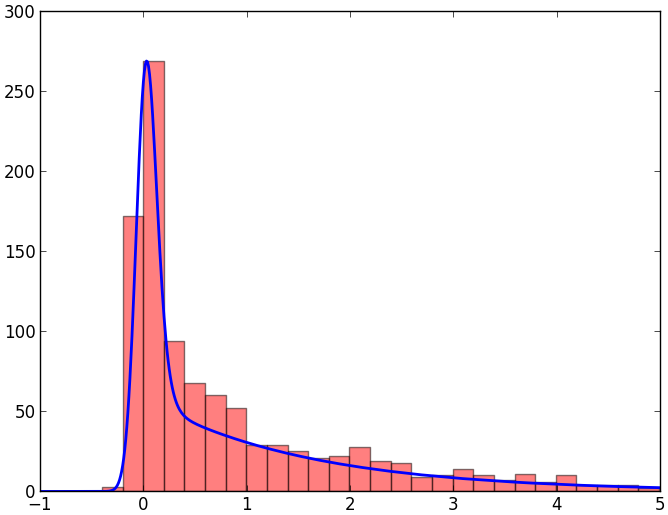
結果のヒストグラム:
)を生成
) が分布関数内に入っていれば、
を分布に従う乱数として採用(下図でいうと赤点が採用、×が不採用)
、
を
に従う一様分布と仮定した時に、